Ruch w miastach: Paradoks Braessa

W 1908 powstał pierwszy seryjnie produkowany samochód Forda. Data ta uznana jest za początek motoryzacji dostępnej dla ogółu społeczeństwa. Od tego momentu rola samochodów osobowych rosła. Dziś, po ponad stu latach eksperci, władze i społeczności same wyciągają wnioski, czy analizują korzyści oraz wady transportu indywidualnego i decydują się na ograniczenie jego znaczenia w pewnych rejonach.

Jest to temat drażliwy w wielu miastach, także w polskich i stale kierowane są argumenty o dalszym poszerzaniu dróg, budowie nowych tras czy wielkich parkingów. Kierowcy przeciwni są zwężaniu dróg czy przeznaczaniu ich na deptaki. Również zabiegi prowadzone dla spowolnienia ruchu nie są dobrze przyjmowane. Często pojawiają się opinie, że bezpieczeństwo zapewniają szersze pasy ruchu i szersze drogi, a nowe trasy oraz poszerzanie dróg likwidują korki. Czy jest tak naprawdę?

Paradoks Braessa

Dietrich Braess to niemiecki matematyk, urodzony w Hamburgu, pracownik wydziału matematyki na uniwersytecie w Bochum. Zasłynął pracą badawczą stworzoną w 1968 roku na temat planowania transportowego o tytule „Über ein Paradoxon aus der Verkehrsplanung”. Przedstawił on w niej analizę sprzeczną z intuicją, mówiącą o możliwości zachodzenia sytuacji, w której zbudowanie nowych tras w mieście pogarsza sytuację dla wszystkich użytkowników dróg. Nowa inwestycja powodować może zwiększenie czasu przejazdu w całej sieci drogowej miasta.

Jak działa paradoks?

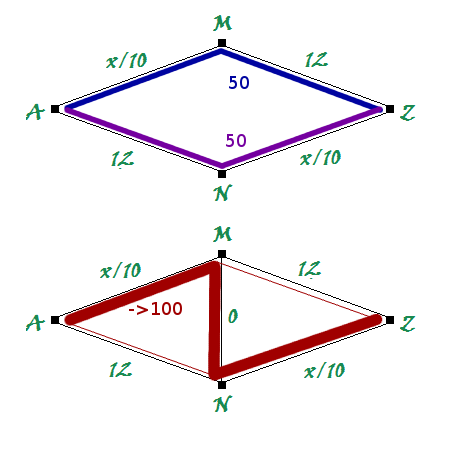
Na podstawie tekstu D. Braessa oraz opracowania Fana Chunga i Stephena J. Younga z Uniwersytetu Kalifornijskiego opisaliśmy działanie paradoksu w uproszczeniu. Załóżmy następującą sieć:

Przyjmijmy, że mamy w niej 100 pojazdów. Pod każdą z krawędzi – dróg – zapisaliśmy czas przejazdu. Czas przejazdu drogami A-N i M-Z jest stały i wynosi 12 jednostek. Czas przejazdu x jest zależny od ilości pojazdów wybierających ulice A-M i N-Z. Rysunek górny prezentuje sytuację wejściową. W tym przypadku połowa kierowców wybiera trasę przez punkt M, a połowa przez N – zgodnie z tzw. Równowagą Nasha, według której każdy dąży do minimalizacji własnego kosztu. Czas przejazdu obiema trasami wynosi w tym przypadku 17 minut.

Do istniejącej sieci dobudowano nową trasę M-N. Przyjmijmy, że jest to trasa szybkiego ruchu lub punkty M i N są blisko siebie i czas jej przejazdu jest znikomy, poniżej 2 minut (na rysunku zaznaczony jako dążący do zera). Postawmy się w roli kierowcy jadącego z punktu A do punktu Z:

W przypadku wyboru drogi „dolnej” – A-N – czas przejazdu wynosi 12 minut. W przypadku drogi „górnej” A-M wynosi on w skrajnym przypadku, przy 100 kierowcach wybierających tę trasę, 10 minut. Oczywiste jest więc, że prawie wszyscy wybiorą wariant A-M. W punkcie M kierowca ma do wyboru dwie możliwości: jechać trasą M-Z przez lub trasą M-N-Z. Czas przejazdu według drugiej możliwości jest niższy stąd znów prawie wszyscy wybiorą tę trasę (przejazd potrwa ok. 10 minut). Rezultat? Najszybciej odcinek A-Z kierowcy przejadą w około 20 minut, a więc wolniej niż bez powstałej trasy M-N.

„Cena anarchii”

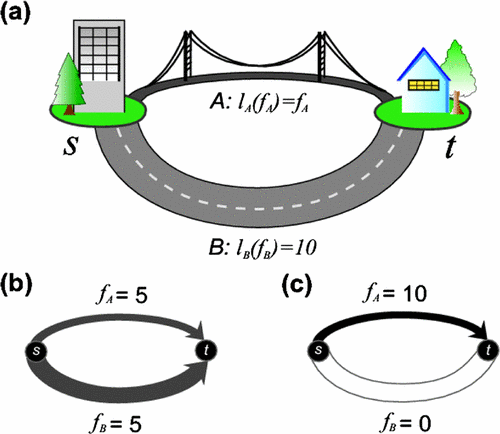
Artykuł Hyejina Youna z koreańskiego Daejeon, Michaela T. Gastnera z Santa Fe oraz Hawoonga Jeong z Uniwersytetu w Albuquerque przedstawia nam kolejny dowód na zajście paradoksu. Według ich pracy nieskoordynowane jednostki w społeczeństwie, dążą do osiągnięcia rozwiązania najkorzystniejszego dla siebie, co nie jest jednoznaczne z rozwiązaniem najkorzystniejszym dla całej społeczności. Za brak skoordynowania jednostek, wszyscy muszą płacić „Price of Anarchy”. Autorzy zaprezentowali też symulację przedstawiającą to nieskoordynowanie: sytuację przy 10 użytkownikach podróżujących z punktu S do punktu T. W skutek dążenia do indywidualnych korzyści kierowcy wybiorą most, przez co ich łączny czas przejazdu wyniesie 100 minut. Społeczne optimum gdzie nie każdy wybierze most, wynosi natomiast 75 minut.

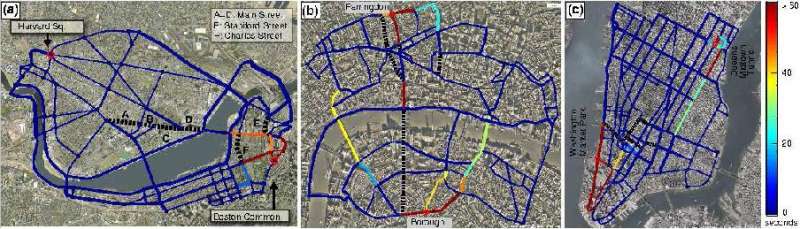
Autorzy wykonali obliczenia dla Bostonu, Nowego Jorku i Londynu. Poniższy schemat przedstawia jak w każdym z miast zamknięcie ulic mogłoby wpłynąć na… przyspieszenie ruchu.

Wyobraźmy sobie, że „most” z grafiki to droga przez miasto. Jak widać kierowcy pomimo funkcjonowania autostrady je omijającej wybiorą drogę przez miasto dla osiągnięcia indywidualnych korzyści. Jakie działania należy podejmować w takich sytuacjach? Przykłady Londynu czy miast skandynawskich (Sztokholmu, Göteborga, Bergen, Oslo, Trondheim) pokazują, że jednym z rozwiązań jest wprowadzenie opłaty za wjazd do centrum miasta. Pozwala ono miastom na zbliżenie organizacji ruchu do poziomu optymalnego dla całego społeczeństwa.

Jak to działa praktycznie?

Dla wielu osób Paradoks Braessa może brzmieć niewiarygodnie, jednak na świecie mamy wiele przykładów, że niesą to tylko obliczenia teoretyczne. Na naszym portalu pisaliśmy już o likwidacji estakad Cheonggyecheon oraz innych tras w koreańskim Seulu. Ich zburzenie nie tylko nie spowodowało zatorów w mieście, ale także zmniejszyło ruch samochodowy w mieście. Rozbudowa sieci drogowej w latach 60-tych w niemieckim Stuttgarcie zwiększyła czasy przejazdów w całym mieście i dopiero likwidacja zbudowanych tras ograniczyła zatory i poprawiła ruch. Podobne zjawiska zaszły podczas zamknięcia ulic w Nowym Jorku oraz Winnipeg.

O interesującym przykładzie z Nowego Jorku napiszemy jeszcze w tym tygodniu!

Czy paradoks Braessa zachodzi w Polsce?

Dokładnych badań nie ma, jednak zamknięcie ulicy Świętokrzyskiej w Warszawie, a więc znaczne utrudnienie dostępu do mostu Świętokrzyskiego, a także zamknięcie dla ruchu indywidualnego mostu Śląsko-Dąbrowskiego nie spowodowało spodziewanego paraliżu na drogach stolicy. Z informacji z kilku polskich miast wynika, że samorządy i zarządy infrastruktury transportowej przy symulacjach nie uwzględniają paradoksu Braessa.

Przy planowaniu siatki drogowej w mieście warto pamiętać, że nie zawsze więcej dróg = lepiej i niezbędne jest przeprowadzenie analiz przed inwestycjami, szczególnie tymi drogimi. Poza paradoksem Braessa działają też inne interesujące zależności – o nich napiszemy niedługo.

Źródła:

1. Youn H, Gastner MT, Jeong H (2008), Price of anarchy in transportation networks: Efficiency and optimality control link

2. Braess D. Über ein Paradoxon aus der Verkehrsplanung link

3. Chung F., Young S. Braess's Paradox in Large Sparse Graphs link